An Introduction to Microsimulation Tax-Benefit Models

Introduction

As we’ve mentioned, the modelling and analysis we’ll be doing here mostly uses data from the UK Family Resources Survey (FRS). The FRS is one of several large household survey datasets for the UK - you’ve already encountered one example when examining the Gender Pay Gap in Block 1.

Each dataset has its own speciality, for example:

• the Wealth And Assets Survey (WAS)¹ - this contains very detailed information on household wealth - the value of houses, pension funds, savings and the like;
• Living Costs and Food Survey (LCF)² - this concentrates on recording household expenditure. One if the LCF’s main uses is providing the weights used in compiling the various measures of inflation, including the Consumer Price index and Retail Price Index.
• Understanding Society³ - this tracks a sample of people each year, recording their health, incomes, and social attitudes.
• English Longitudinal Survey of Ageing (ELSA)⁴ - like US, this is tracks a sample elderly people over time, with specialised questions on health, social care and the like.

There is a good deal of overlap between all of them - all need the same basic demographic information - people’s ages, gender, employment status and so on, and all ask at least some basic information on income and wealth, though the FRS goes into much more detail on incomes and WAS on wealth. All of them have been used in various specialised microsimulation models.⁵

By the standards of modern ‘Big Data’, our datasets are relatively small - a few thousand households⁶ rather than the millions of observations available to the likes of Google or Facebook, but they more than compensate for this in the richness, accuracy and detail of what’s recorded.

All these major surveys are collected face-to-face using trained interviewers⁷. This is expensive, but necessary given the very complex material collected. All except ELSA are surveys of households - they skip, for example, rough sleepers, people in care homes, barracks, prisons and the like. (ELSA follows people to care homes). They all aim to to be representative samples of UK households⁸, usually by picking addresses randomly from complete lists of all UK addresses⁹. The list of all the things that could be sampled is known as the sample frame, and the proportion of addresses picked is known as the sample frequency: if we pick one household in every 5,000, the sample frequency is 1/5000 = 0.0002.

The FRS, WAS, and LCF are cross-section surveys - each year a new set of households is surveyed. Understanding Society and ELSA, are Longitudinal¹⁰ surveys, where the same people are re-interviewed each year. Longitudinal surveys have advantages. For example, in the econometric modelling you came across earlier, there is always the worry that the variation in the thing you’re trying to explain (the ‘dependent variable’) is because of things you can’t observe in your dataset, such as tastes, attitudes and the like (‘unobserved heterogeneity’ in the jargon); it’s often possible to exploit the structure of a panel dataset to eliminate this heterogeneity, and so focus in on just systematic influences. But this power comes at a cost. It’s much more expensive to gather a Longitudinal dataset than a cross-section of the same size. With a Longitudinal dataset, if one your subjects decides to go to live in the other end of the country, you have to send your interviewer after them. With cross sections, it’s usually good enough to pick streets or blocks of flats at random, and then interview a bunch of people in that street - “stratified sampling” rather than “random sampling”. Also, since it’s very important to keep people in the Longitudinal survey for as long as possible, there’s a tendency not to ask the kinds of burdensome questions about incomes, spending or wealth that the cross-sectional surveys might get away with once.

Mostly, our surveys ask questions about the household in a given month or week, with a few questions about how the household has been faring in the longer term. With Longitudinal data, of course, we can look back at previous years to get a picture of how things have evolved over time.

Grossing Up and Non-Response

If a sample survey is truly representative of the population we can multiply up the data by the inverse of the sample frequency to get population estimates. If we see, say, 200 people in the survey with a certain disability, and the sample frequency is 1/2000, our best estimate is that there are 400,000 (2,000×200) such people in the country. In microsimulation, this step is know as grossing up, and the number we’re multiplying our sample by (2,000 in this example) is known as the grossing factor.

However, these surveys are voluntary; unlike the Census, no-one can be compelled to participate in the FRS or LCF, and indeed only about 50% of those approached agree to. (Participation in the Family Expenditure Survey, the predecessor to these surveys, was over 80% in the early 1960s, but participation has declined steadily ever since)¹¹. If non-participation was random, this wouldn’t pose much of a problem, but in reality some types of household are much less likely to participate - those with high incomes, or sick or disabled members, for instance. In microsimulation jargon, this is response bias. A way around this is differential weighting. If, because of response bias, a dataset sampled 1 in every 100 working aged adults, but 1 in 200 pensioners, we could simply gross up each working aged person by 100, but each pensioner by 200, and that would give us the correct total for each group. For this to work, of course, we need some external source of information on what the actual number of pensioners and working age adults should be; information like this typically comes from the Census (which should include everybody) or other official sources such as tax-returns or the electoral roll. In practice things are more complicated than this, because there is response bias in multiple dimensions - not just by age, but also income, health, location, and other characteristics. Methods exist that can calculate weights that will allow a dataset to be grossed up so as to give correct totals for multiple sets of targets.¹² The model you will be exploring presently uses such a set of weights[^FN_ATTRITION].

Dealing with Uncertainty

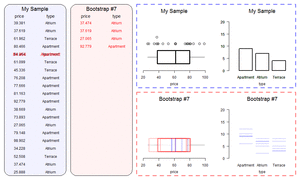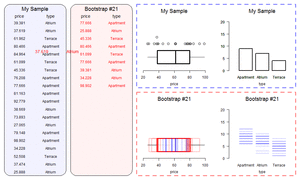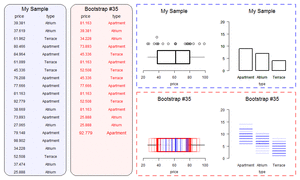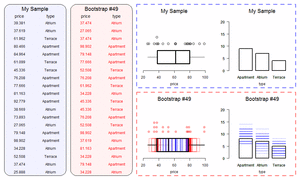
If the re-ran our sampling procedure, randomly picking different households, we would likely get a slightly different number for our estimate of disabled people. So we can’t be certain that 400,000 is the true number. We can use statistical theory to quantify the uncertainty around our estimate. We’re not able to discuss the mechanics of this in detail here, but, broadly, the larger the sample and the smaller the amount of variation in our dataset, the more confidence we can have in our estimate¹³. The uncertainty is often expressed using “confidence intervals” (sometimes called the “margin of error” in popular discussions). Confidence intervals have a slightly unintuitive interpretation: roughly, if we re-ran our sampling many times, and calculated our confidence interval each time, the true value would be inside the interval in 95% of the samples. For simple cases like this, where we want the uncertainty surrounding an estimate there are usually nice formulas we can apply. But a microsimulation model might need information from dozens of variables (for wages, hours of work, and so on), and there might be other sources of uncertainty such as how people’s behaviour responds to tax changes. In these cases, there may be no simple formula that we can use to calculate our confidence intervals. Instead, we often estimate uncertainty using bootstrapping. Bootstrapping involves running our calculations many times, each with as slightly different sample dataset, and perhaps also with different assumptions about behavioural responses. You can simulate a different sample by deleting a few observations randomly on each run¹⁴. The little simulation below shows a simple simulation of bootstrapping a sample dataset.

Other Problems with large datasets

There are other difficulties we should briefly mention:

Firstly, some people might be reluctant to answer some embarrassing questions. When grossed up, the LCF records spending on smoking and drinking that are of about half the level suggested from official tax statistics¹⁵. This is under-reporting. (There may be other reasons for the survey estimates being too low, for example, a lot of smoking and drinking may be by non-households, such as tourists, and so outside the sample frame). Particularly important for out purposes is possible under-reporting of high incomes. In most official estimates of poverty and inequality, such as the HBAI estimates we discussed earlier, the incomes reported by the very richest people in the FRS are considered so unreliable that they are replaced entirely by imputed incomes derived from income tax records¹⁶.

Secondly, even if we have the right sample, and even if the questions are answered accurately, the questions might be the wrong ones for the purposes of a microsimulation model. For example, in the FRS, the questions asked about wages and salaries are pretty close to those asked on a tax-return or benefit application form, but the questions on self-employment incomes are far from what’s needed for an accurate tax calculation.